How many lives does a doctor save? (Part 2)

This is Part 2 of an updated version of a classic three-part series of 80,000 Hours blog posts. You can also read updated versions of Part 1 and Part 3. You can still read the original version of the series published in 2012.
In the last post, we saw that although the reasons people live longer and healthier now have more to do with higher living standards than more medical care, medicine still plays a part. If you try and quantify how much medicine contributes to our increased longevity and health, then divide that amount by the number of doctors providing it, you get an estimate that a UK doctor saves ~70 lives over the course of their career.
Yet this won’t be a good model of how much good you would actually do if you became a doctor in the UK.
For one thing, the relationship between more doctors and better health is non-linear. Here’s a scatterplot for each country with doctors per capita on the x-axis and DALYs per capita on the y-axis (since you ‘gain’ DALYs for dying young or being sick, less is better):
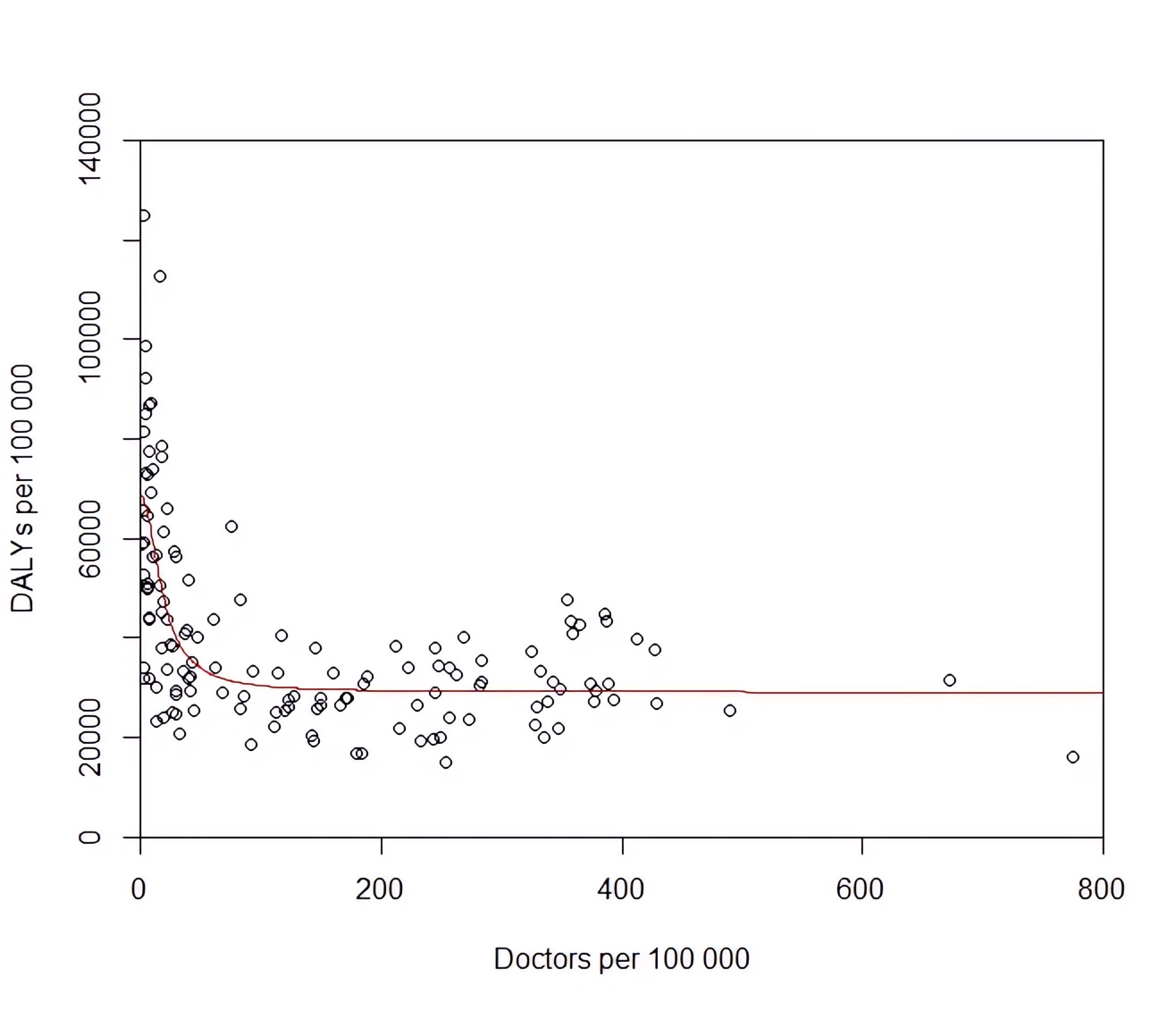
The association shows an initial steep decline between 0–50 doctors per 100,000 people, then levels off abruptly and is basically flat when you get to physician densities in richer countries (e.g. the UK has 300 doctors per 100,000 people). Assuming this is causation rather than correlation (more on that later), adding more doctors has diminishing marginal returns for population health.
In other words, the first doctors added to a population have a much larger impact than those added later.1
This makes intuitive sense. When I left clinical practice in the UK, there wasn’t a ‘Greg-shaped hole’ in the health service. Rather, the health service and the remaining doctors will engage in triage, taking over the most important things I would have done at the expense of the least important things they were going to do. So the ‘hole’ made by my departure was much smaller than you might naively think.
You can use this kind of reasoning to work out the impact you would make as a doctor, as you’ll usually be working somewhere which has a lot of doctors already. Even if you become a trauma surgeon or emergency physician providing life-saving care, it will seldom be the case that those lives saved depended on you entering medical school.
Counterfactually, there would have been another doctor doing this in your place, and your addition is, at best, a marginal improvement. For example, a better-staffed emergency room can respond to major cases a little quicker (which sometimes makes a big difference) or can treat minor injuries a little better. This certainly matters, but the impact is less impressive than it first appears.
We can use the graph above to put this quantitatively. If we used the observed relationship between health improvements and proportion of physicians in a population, we can infer the impact you have by being the next additional doctor joining the profession:
- The best fit line gives 26,678 DALYs per 100,000, with 300 doctors per 100,000 (as it is in the UK). If you’re the 301st additional doctor, the DALYs figure is just a tiny bit smaller — 26,673.2
- This is a difference of 5 DALYs, so a population with you as an additional doctor suffers 5 DALYs fewer each year you work.
- As this is a yearly rate, one should multiply by career length. At 40 years, 40×5 = 200 DALYs averted during a medical career.
Two hundred is about 10 times less than 2,100, so with the same conversion rate of 30 DALYs for one life saved, you are saving about seven lives over your career, rather than 70.
But even this more modest figure is still an overestimate.
Confounding and causation
One reason comes from the last post. The calculation I just did implicitly assumes that a population’s health is solely determined by how many doctors it has. Yet, as seen earlier, a lot of what determines a population’s health are social determinants rather than medical care.
Wealth itself is a major confounding factor. Richer populations are healthier for many reasons, and they can also afford more doctors. But it’s their wealth, rather than their greater access to doctors, that largely explains why they are healthier.
Disentangling the causal impact is tricky,3 but I had a go in my master’s dissertation.4 I looked at international data on population health and number of doctors and measured other determinants like wealth and education, plugging all the factors into a regression model. This helps approximate the marginal impact of a doctor when you control for obvious confounding variables.
I found that there remains an association between countries with more doctors and countries with less burden of disease. However, this relationship is smaller and not statistically significant.
If we take the data at face value anyway and ignore that it’s not statistically significant, the impact of a doctor in the UK falls by roughly half: ~2.5 DALYs per year, ~100 DALYs per career.
In other words, this analysis shrinks our estimate of ‘several lives saved’ to ‘a few lives saved.’
The real number is almost surely lower
This analysis remains very rough, but the estimated impact keeps falling as you account for other obvious factors. I am pretty sure we are approaching the real value of a doctor’s impact ‘from above’ — that is, I expect further improvements to the quality of analysis to result in lower bottom-line figures.
For example, here are two more large downward corrections we should be making:
- Doctors are not the only profession providing healthcare: nurses, allied health professions, diagnostic lab staff, and many others also play a role. So all the benefits of healthcare should not be attributed to doctors alone as we’ve done so far. This is hard to put numbers on, but I’d be surprised if doctors can take more credit for medical care than everyone else working in healthcare put together. This suggests dividing the estimate by at least two.
- Medical schools have a basically set number of places and entry is competitive. So while talking about adding or removing an additional doctor makes sense for people already in medical school (or already practising), it makes less sense for those thinking of applying to medical school. Counterfactually, if you don’t apply, your place will be filled by another applicant. There is still some impact: (e.g.) adding more applicants to the pool means medical schools can be more selective, so drawing (in expectation) a class of slightly better future doctors (assuming that the application process is good at selecting for candidates who will be high-quality doctors!). This impact seems a lot less than if your decision to enter medicine actually resulted in an additional doctor — again, we should probably divide the estimate by at least two.
Given all of this, perhaps a better guestimate of the impact of becoming a doctor in a place like the UK is something like one DALY averted each year you work, so maybe one or two ‘lives saved’ over your career.5
How my chequebook beat my stethoscope
Although this was a far cry from my first impression (or medical dramas where the protagonists are saving lives every episode), saving a couple or a few lives over my career still looked worthwhile to me.
But while I wrote I wanted to do something worthwhile when I applied to medical school, I also wrote about applying myself to do the most worthwhile thing I could do. I figure I’m not alone in being interested in how the impact of being a doctor stacks up compared to other contributions you could make, so here’s an illustration.
After graduating medical school I started work as a junior doctor. Using the regression model to guess my impact (and ignoring the further corrections I noted, as well as the fact that rookie doctors like me would tend to contribute less than the typical doctor) my first year working in the UK maybe averted something like 2.5 DALYs, or ~0.1 lives saved.6
I am also a member of Giving What We Can,7 so — as I was now earning money — I could start giving some of it to charity like I promised. I managed to give around £10,000 in my first year of doctoring. Taking all manner of liberties, we could guess:
- I gave around half to highly effective global health charities, and half to support more speculative research. Discount the latter as too hard to quantify, so £5,000.
- At 2013 exchange rates, £5,000 was about $8,000.
- Estimates of cost-effectiveness of top global health charities have changed over the last decade, both in terms of preferred metrics, preferred charities/interventions, and point estimates. Hopefully, some of that is due to diminishing marginal returns (i.e. 2013’s ‘best buys’ for global health were bought, so ‘second-best buys’ in 2013 move up to the top of the list in 2023), but some of it is likely due to better assessment and clearer understanding. Let’s ignore these caveats and look at current GiveWell top recommendations,8 which suggest donations can save a life for ~$5,000
- So if we divide 8,000 by 5,000, we come to an estimated 1.6 lives saved.
So, despite being pretty generous to my clinical work (and not so generous to my charitable giving), my donations did more than 10 times as much good as my year working as a doctor. A more even-handed comparison might find the impact of my first year of fulfilling my Giving What We Can pledge roughly matched the direct impact I could expect to make over my entire medical career.
The donations also seemed a lot easier: £10,000 is a lot of money, but medicine is fairly well paid. Even at the bottom of the medical salary scale, and net these donations, I was still better off than the median person in the UK (and in the top few percent globally). If I stayed in medicine, I’d end up much better off even if I continued giving similar proportions as my salary grew.
Having found medicine did not stack up well against donations, I planned to tilt my medical career to do more good via this more effective means. My idea was to pick a specialty which was lucrative that I could be good at, so I could:
- Earn more money
- Give more of it away
- And do more good — saving more lives with my chequebook than with my stethoscope. )
Yet I didn’t end up doing this — a career strategy called ‘earning to give‘ — and instead ended up doing something else I hope and expect is even better still. We’ll look at a number of ways one could do more good as a doctor (or perhaps instead of being a doctor) next.
Read next: How many lives does a doctor save? (Part 3)
What could a doctor do to really save a lot of lives? Would another career path altogether be better?
Learn more:
- Read our in-depth career guide
- Problem profile: Preventing catastrophic pandemics
- Career review: Biorisk research, strategy, and policy
- Podcast episode: Dr Pardis Sabeti on the Sentinel system for detecting and stopping pandemics
- Podcast episode: Elie Hassenfeld on two big picture critiques of GiveWell’s approach, and six lessons from their recent work
- Podcast episode: Andy Weber on rendering bioweapons obsolete and ending the new nuclear arms race
Notes and references
- The diminishing marginal returns do not just apply to doctors but most proposed ‘inputs’ into better health generally. The canonical example is the Preston curve of life expectancy versus GDP per capita:
- The best fit line I used was a simple reciprocal: DALYs = 50,000 / (8.96 + Doctors) + 25,060. One could definitely argue over which functional form (logistic, exponential, something else?) is more reasonable in theory or gives the best fit in practice, but it’s clear that whatever curve you pick will be very flat in this region of the scatter plot.
You could also argue over the right interval to compute marginal return. Should it be three vs four doctors per 1000, 300 vs 301 doctors per 100,000, or ~210,000 vs ~210,001 doctors in the UK? As the best fit line is convex, smaller intervals give bigger effects as they better approximate the derivative. In theory, perhaps the choice turns on how ‘granular’ or not you think responses on the margin can be — i.e. my departure may have affected more than three other doctors and 1000 people, but probably not every other doctor and patient in the country. In practice, the curve is so flat (and other sources of error so significant) it doesn’t really matter much; the difference will be +/- 20%.↩
- Inferring causation from observational data is known to be treacherous, and there are a few things which make this even more treacherous here:
- Everything is correlated to everything else (multicollinearity). Number of doctors correlates with health, but so does GDP, measures of education, and measures of sanitation — and they all correlate with one another. So isolating the impact of a single predictor (i.e. number of doctors) is fraught. A similar problem applies when working out historically the relative importance of different factors. Although we can rule against medical care being a big contribution, attribution between nutrition, wealth, and public health measures is difficult as all these putative explanatory variables were changing at roughly the same time.
- Limited data: every country in the world only gives you around 200 data points. This does not give much information to pin down the relative effect sizes of multiple variables influencing the outcome at once. Include too many possible factors, and you risk overfitting.
- Omitted variables: Leaving too many potential variables out is not safe either (omitted variable bias). In the same way we might overestimate the impact of doctors if we do not include the likely confounding factor of GDP per capita, if you miss important factors the analysis will misattribute their impact to things you do include.
All of this adds up to a lot of uncertainty (but hopefully not too much directional bias). Yet we can only play the hand reality dealt us.↩
- A slightly more detailed recipe:
1. Pick DALYs per 100,000 as the outcome variable
2. Pick (a priori) potential explanatory factors: Doctors, Wealth, Education, Sanitation, and Inequality.
3. Then I found variables for these factors which get reported in international data. For some this is easy (e.g. GDP per capita for wealth), for others you take a couple of measures and use the first principal component to get a combined score (e.g. for education, take adult literacy, primary school completion percentage, and proportion entering tertiary education).
4. Use multiple imputation with chained equations on the missing data
5. Transform these independent variables if necessary to make their relationship to the dependent variable (DALYs per 100,000) roughly a straight line. (E.g. DALYs per 100,000 versus GDP per capita looks like a preston curve; DALYs per 100,000 versus ln(GDP per capita) looks like a straight line).
6. Plug this into ordinary least squares regression.↩ - This line of argument assumes that the rest of the world stays static. If everyone who wanted to become a doctor in the UK read these posts and decided to do something else, we’d eventually find ourselves in a situation where adding an additional doctor to the field could probably do a lot more good. I doubt I am that persuasive, but this is why the issue of coordination is so important in altruistic career selection.)↩
- For what it is worth, this roughly matches my experience of that year working: I cannot think of any dramatic life-saving movements where I was making the critical difference. I think I did do useful work, and I think that added a few small counterfactual increments, but if anything 2.5 DALYs feels generous.↩
- Giving What We Can, like 80,000 Hours, is a project of the Effective Ventures group.↩
- Open Philanthropy, 80,000 Hours’ largest funder, was spun out of GiveWell, and the organisations share some leadership.↩